- 등각항로의 정확한 방위/거리를 구하는 방식 발견
- 상식과지식/일반상식
- 2009. 7. 25. 04:17
앞에 포스팅했던 지구 타원체에서 두 점간의 방위와 최단거리 계산하기를 쓰면서 프로그램을 하나 만들었다.
지표면 상에서 두 좌표 간의 방위와 거리를 각각 대권항로와 등각항로로 계산해주는 프로그램이다.
그런데, 문제가... 대권항로는 WGS84 좌표계에서 계산을 하는데, 등각항로는 사실 WGA84 타원체의 평균반지름을 반지름으로 갖는 구체에서 계산한다는 것이었다.
(이렇게 계산하면 최악의 경우 0.55%까지 거리의 오차가 발생한다)
오늘... 드디어... WGS84 타원체 상에서 등각항로의 방위와 거리를 정확하게 구하는 방식을 발견했다.
(아쉽게도 논문 같은 것은 찾지 못했음)
Juhani Kaukoranta님께서 Navigation, Astronavigation, Positioning and Geodesy라는 페이지에 식을 포함한 각종 자료를 올려주셨더라.
역시 수학은 멋지고 위대하다.
이 방식을 공부해야겠다!!!

지표면 상에서 두 좌표 간의 방위와 거리를 각각 대권항로와 등각항로로 계산해주는 프로그램이다.
그런데, 문제가... 대권항로는 WGS84 좌표계에서 계산을 하는데, 등각항로는 사실 WGA84 타원체의 평균반지름을 반지름으로 갖는 구체에서 계산한다는 것이었다.
(이렇게 계산하면 최악의 경우 0.55%까지 거리의 오차가 발생한다)
오늘... 드디어... WGS84 타원체 상에서 등각항로의 방위와 거리를 정확하게 구하는 방식을 발견했다.
(아쉽게도 논문 같은 것은 찾지 못했음)
Juhani Kaukoranta님께서 Navigation, Astronavigation, Positioning and Geodesy라는 페이지에 식을 포함한 각종 자료를 올려주셨더라.
역시 수학은 멋지고 위대하다.
이 방식을 공부해야겠다!!!

친절하기 짝이 없는 설명의 일부 ^^;
'상식과지식 > 일반상식' 카테고리의 다른 글
| 러시아 국가는 안 바뀐 게 아니었다 (3) | 2012.02.15 |
|---|---|
| 태극기 좀 바르게 그리자! (10) | 2010.04.24 |
| 지구 타원체에서 두 점간의 방위와 최단거리 계산하기 (9) | 2009.07.21 |
| Bessel 타원체와 WGS84 좌표계 (8) | 2009.07.19 |
| 메르카토르 도법에 대한 어이없는 오해 (9) | 2009.07.19 |




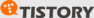
Recent comment